评价偶然因素在科学试验中可能发挥的作用
在解读科学试验中有关疗效比较的结果时,偶然因素会让我们犯两种错误:当实际疗效无差异时我们错误地认为有差异,或是实际疗效有差异而我们没有发现。被观察的特定治疗效果其样本量越大,上述错误发生的几率就越小。
考虑到疗效比较不可能将以往接受过或是未来将要接受治疗的所有个体包括在内,所以完全揭示两种治疗方案“真实的差异”是不可能的。但是,科学研究必须对这种真实的差异做出最佳的推测。
“可信区间”(Confidence Interval, CI)常用来表示估算出的差异的可信程度。它给出了真实差异可能存在的范围。即便不提可信区间这称谓,相信大多数人也知道它是什么。
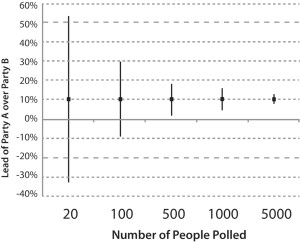
“可信区间”(Confidence Interval, CI)常用来表示估算出的差异的可信程度。它给出了真实差异可能存在的范围。即便不提可信区间这称谓,相信大多数人也知道它是什么。比如,在选举筹备阶段,一项民意调查显示A政党领先B政党10%的支持率;但如果我们留意媒体报道的话,我们会发现这两个政党支持率的差距最小可能5%,而最大能达到15%。上述的“可信区间”表明两政党的真实差异可能会落在5%~15%之间的某一点。
随着越来越多的受调查者参加,结果的不确定性也越来越小,而两党支持率差异的估计值所对应的可信区间也就越窄。
就像我们能通过两个政党支持者的比例估算出两党支持率差异,进而得出该差异的不确定程度一样,我们同样也可以通过患者接受两种治疗后其病情缓解或恶化的人数之比估算出疗效差异,进而得出该差值的不确定程度。
再举个例子,对比两种方案治疗心脏病的效果,观察的治疗结果数量越多,评价疗效差异的可信区间就会越窄。而可信区间“越窄越好”。
通常会有一项指标来说明我们有多大把握认为真实值会落在可信区间的估计范围内。例如,95%的可信区间意味着无论真实值是什么,我们都有95%的把握认为真实值会落在可信区间范围内。这也意味着,每100个“真实”值里可能会有5个(5%)落在范围外。